
Module 13 - Recursion and Recursive Functions
Topics in
this Module
Introducing Recursion
What is Recursion?
Recursion is a programming technique in which a function calls itself to solve a problem. In other words, a function that calls itself is known as a recursive function, and the process of a function calling itself is called recursion. Recursion is a powerful concept used in various algorithms and problem-solving scenarios.
Basic Example of Recursive Function: Factorial:
Let's start with a simple example of a recursive function to calculate the factorial of a positive integer.
def factorial(n):
if n == 0 or n == 1:
return 1
else:
return n * factorial(n - 1)
Explanation:
The factorial() function takes an integer n as input.
If n is 0 or 1, the function returns 1 as the factorial of 0 and 1 is 1.
Otherwise, the function returns the product of n and the result of calling factorial(n - 1), which calculates the factorial of the previous number.
Using the Recursive Factorial function:
print(factorial(5)) # Output: 120
print(factorial(0)) # Output: 1
print(factorial(1)) # Output: 1
Another Example of Recursion
Advanced Example of Recursive Function: Fibonacci Sequence:
The Fibonacci sequence is a series of numbers where each number is the sum of the two preceding ones. Let's create a recursive function to calculate the nth number in the Fibonacci sequence.
def fibonacci(n):
if n <= 0:
return "Invalid input. Please provide a positive integer."
elif n == 1:
return 0
elif n == 2:
return 1
else:
return fibonacci(n - 1) + fibonacci(n - 2)
Explanation:
- The fibonacci() function takes a positive integer n as input.
- If n is less than or equal to 0, it returns an error message.
- If n is 1, the function returns 0, as it is the first number in the Fibonacci sequence.
- If n is 2, the function returns 1, as it is the second number in the Fibonacci sequence.
- Otherwise, the function returns the sum of the two preceding Fibonacci numbers calculated by recursively calling fibonacci(n - 1) and fibonacci(n - 2).
Example use of Recursive Fibonacci Sequence function:
print(fibonacci(7)) # Output: 8 (0, 1, 1, 2, 3, 5, 8)
print(fibonacci(10)) # Output: 34 (0, 1, 1, 2, 3, 5, 8,
Using Recursion
Use Cases for Recursion:
Recursion is suitable for solving problems where a task can be divided into smaller subproblems, and each subproblem is similar to the original problem but smaller in size. Some use cases include:
- Calculating mathematical series (e.g., factorial, Fibonacci).
- Traversing and searching trees and graphs.
- Solving problems related to dynamic programming.
- Backtracking algorithms (e.g., N-Queens problem, Sudoku).
Considerations and Limitations:
Recursive functions can lead to excessive function calls, potentially causing a stack overflow if the recursion depth is too high. It is essential to have a base case that terminates the recursion.\
- Recursive functions might be less efficient than iterative solutions for some problems due to the overhead of function calls.
- Properly handling base cases is crucial to ensure the termination of recursion and prevent infinite loops.
- Recursion can be challenging to understand and debug, so clear documentation and well-defined base cases are essential.
- Some problems may be better solved using iteration rather than recursion, as it can be more efficient and straightforward to implement.
When to Use Recursion and When Not To:
Recursion is an elegant approach for problems that have a natural recursive structure. It can lead to concise and readable code when the problem is well-suited for recursion. However, there are cases where recursion might not be the best choice:
- Problems that have a straightforward iterative solution (e.g., simple loops).
- Problems that require high performance and memory efficiency, as recursion can incur extra overhead.
- Problems that have deep recursion depth, as it might lead to stack overflow.
- Problems where the recursive solution results in redundant computations and inefficiency.
In conclusion, recursion is a powerful concept in programming that allows solving complex problems by breaking them down into smaller subproblems. It is well-suited for problems with recursive structures, but it should be used judiciously, considering the problem's complexity, efficiency, and stack depth to avoid potential issues.
Nested Lists and Recursion
A very common use of recursion is the exploration of nested lists or linked items to explore them, count them, or catalog them. Below, I've provided an example of this. I've included comments in the code to explain each line, and below that I've provided a more readable explanation of the list structure and the traversal process.The list will be at least three levels deep, and each level will have strings starting with the letters 'A', 'B', 'C', etc.
Explanation of the Nested List:
We'll create a nested list with the following structure:
- At the top level, there will be strings starting with 'A'.
- At the second level, there will be strings starting with 'B'.
- At the third level (deepest level), there will be strings starting with 'C'.
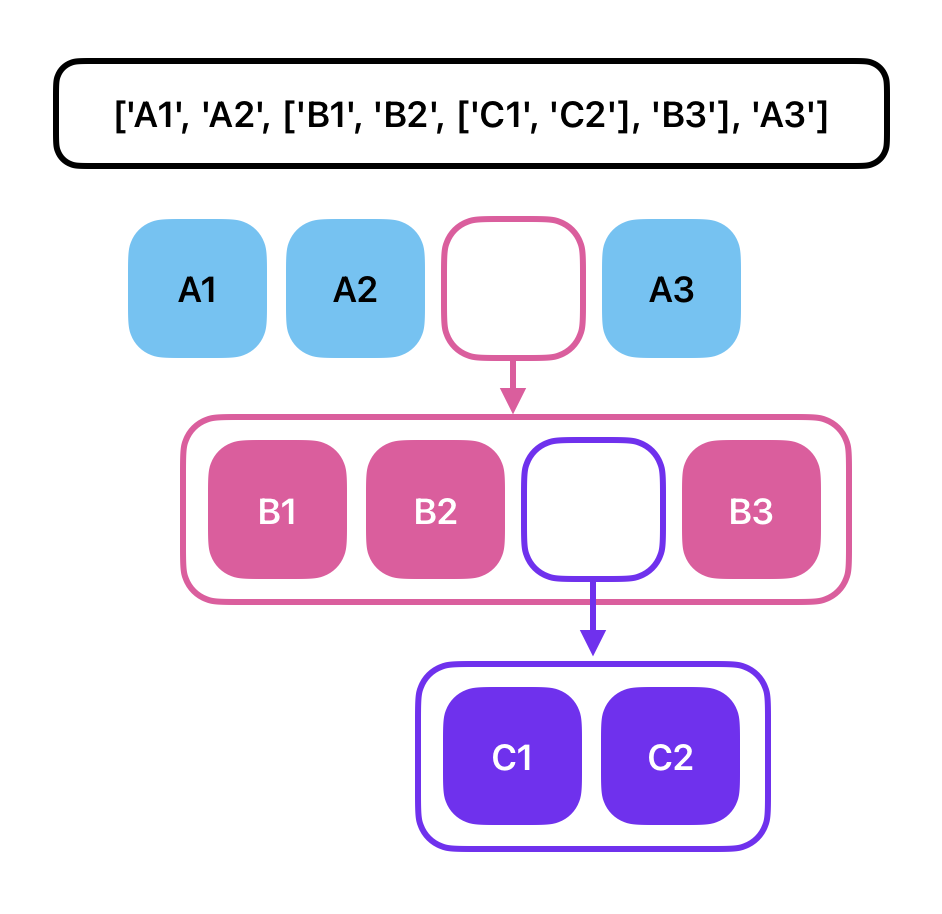
The list structure will look like this:
['A1', 'A2', ['B1', 'B2', ['C1', 'C2'], 'B3'], 'A3']
Here is a diagram that might make the structure a bit more clear:
Explanation of Recursive Traversal:
The recursive function will start at the top level of the list and check each element:
- If the element is a string, it will be counted as a leaf node.
- If the element is a sublist (nested list), the function will call itself recursively on that sublist to explore the deeper levels.
- The process continues until all elements in the nested list are traversed, and the count of leaf nodes is returned.
Python Code with Comments:
def count_leaf_nodes(nested_list): # Initialize the count to 0 count = 0
# Iterate through each element in the nested list for element in nested_list: # If the element is a string, it is a leaf node, so increment the count if isinstance(element, str): count += 1
# If the element is a sublist (nested list), call the function recursively elif isinstance(element, list): count += count_leaf_nodes(element) # Return the total count of leaf nodes return count
# Nested list with strings at three levels deep nested_list = ['A1', 'A2', ['B1', 'B2', ['C1', 'C2'], 'B3'], 'A3'] # Call the recursive function to count leaf nodes result = count_leaf_nodes(nested_list) # Print the result print("Number of leaf nodes:", result) # Output: Number of leaf nodes: 6
Explanation of the Code:
- def count_leaf_nodes(nested_list): - Defines the recursive function count_leaf_nodes, which takes a nested list as input.
- count = 0 - Initializes the variable count to 0. This variable will keep track of the number of leaf nodes.
- for element in nested_list: - Iterates through each element in the nested list.
- if isinstance(element, str): - Checks if the current element is a string (leaf node). If so, increments the count by 1.
- elif isinstance(element, list): - Checks if the current element is a sublist (nested list). If so, calls the count_leaf_nodes() function recursively on the sublist to explore deeper levels.
- return count - After all elements in the nested list are traversed, the function returns the total count of leaf nodes.
- nested_list = ['A1', 'A2', ['B1', 'B2', ['C1', 'C2'], 'B3'], 'A3'] - Defines the nested list as described earlier.
- result = count_leaf_nodes(nested_list) - Calls the count_leaf_nodes() function with the nested list and stores the result in the variable result.
- print("Number of leaf nodes:", result) - Prints the total count of leaf nodes. In this case, the output is Number of leaf nodes: 6.
Note: The recursive function traverses the nested list by exploring each level and counting the leaf nodes along the way. It continues to call itself recursively on sublists until all elements are checked, and the final count is returned.
Videos for Module 13 - Recursion and Recursive Functions
13-1: Introducing Module 13 - Recursion (1:46)
13-2: Fractals as Visual Depictions of Recursion (6:55)
13-3: Explaining Recursion (4:47)
13-4: Recursion Applied to a Real-World Problem (5:02)
13-5: Recursive Tree Traversal Code (6:47)
13-6: Sandbox 13 Explanation (3:50)
Key Terms for Module 13 - Recursion and Recursive Functions
No terms have been published for this module.
Quiz Yourself - Module 13 - Recursion and Recursive Functions
Test your knowledge of this module by choosing options below. You can keep trying until you get the right answer.
Skip to the Next QuestionActivities for this Module
S13 - Playing With Fractals
Fractals are one of my favorite things in math and computer science. They're fascinating because they combine simple patterns with infinite complexity, and they can be incredibly beautiful too! A fractal is a type of pattern that repeats itself on smaller and smaller scales. Imagine zooming in on a picture, and as you get closer, you see the same shape again and again, no matter how much you zoom. This property is called “self-similarity."
What’s truly exciting about fractals is that you can generate them using very simple rules and basic computer programs. For instance, one of the most famous fractals is the Mandelbrot set, which looks a bit like a warty bug and is created by repeating a simple mathematical operation. Despite the simplicity of the rules, the resulting images contain an endless depth of detail, with swirls and patterns emerging out of what started as just a few lines of code.
In computer science, fractals are a great example of how a straightforward algorithm can lead to outcomes that are unpredictably complex and often stunningly beautiful. They teach us about recursion, a concept where a function calls itself with a slightly altered input, which is a critical technique in programming. Moreover, they have practical applications too, such as in computer graphics for creating natural-looking scenery, in antenna theory for designing compact antennas, and even in medicine for analyzing patterns that occur in nature. So, diving into fractals not only expands your understanding of mathematics and programming but also opens up a world of applications that intersect with real-world problems and aesthetics.
One such mathematical pattern in computer science is the Mandelbrot Set. Here is a visualization of it:

Fractals are particularly interesting, because they also occur in nature. Check out my favorite: Romanesco Broccoli. I don’t know how it tastes, but it looks AMAZING.

You can produce fractals in Python, too. Try this code, which produces another famous fractal, the Dragon Curve:
If you look closely, you will see something interesting going on. Inside the main function called draw_dragon_curve( ), you will see calls to a function called draw_dragon_curve( ). Wait a minute. Yep - you read that right. This function calls itself to produce the fractal design. This is because fractals are a visual example of what we call “recursion” in Computer Science.
Recursion, simply put, is a function that calls itself.
Here is a much simpler example, that draws a simple fractal tree:
Play around with the code, and see what sort of interesting things you can produce. Can you make it bigger or smaller? Can you make different sized branches a different color or different line thickness? Can you put some leaves at the end of the smallest branches?